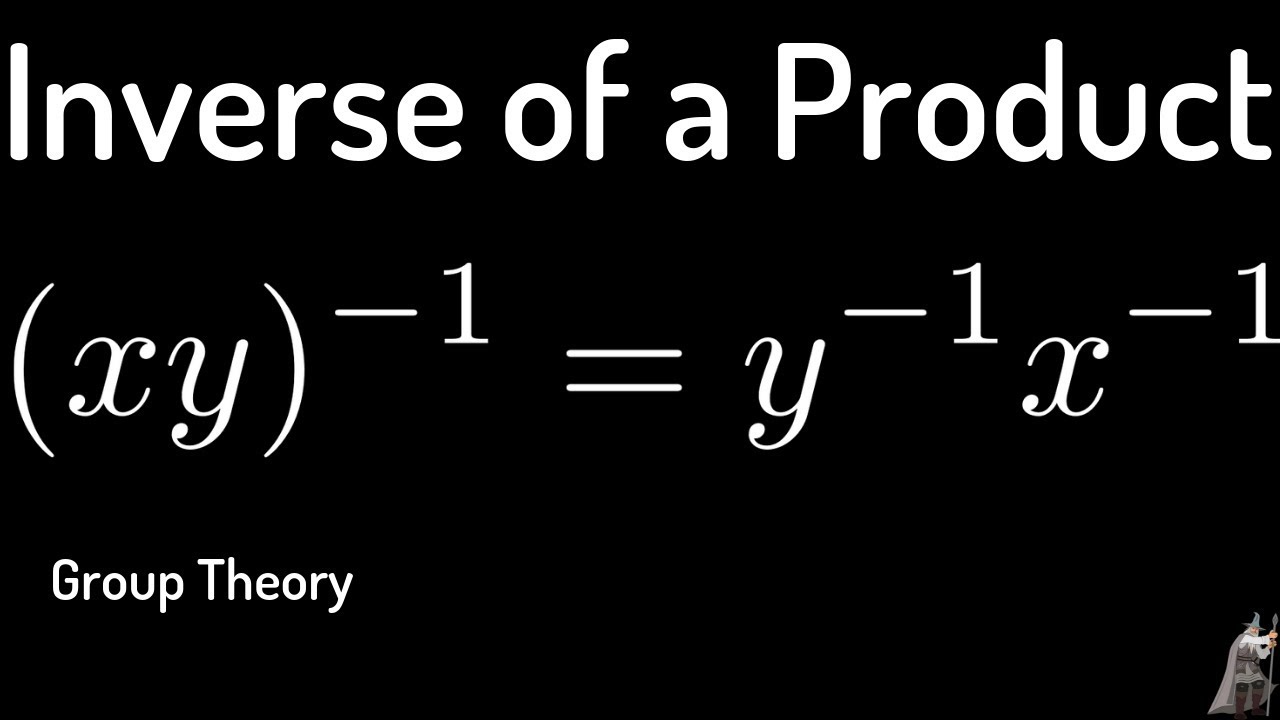Subgroup Proof Examples . The intersection of two subgroups of a group g g is a subgroup of. Then (h, ∘) (h, ∘) is a subgroup of (g, ∘) (g, ∘). For na, nb ∈ nz, na + nb = n(a + b). First, nz is in fact a subgroup. the subgroup \(h = \{ e \}\) of a group \(g\) is called the trivial subgroup. Let h h be a subset of g g. for example, (z=2z) (z=2z) is a group with 4 elements: Let (g, ∘) (g, ∘) be a group. properties of subgroups | emathzone. The additive identity is in nz. Let g be a group and let g ∈ g be an element of g. A subgroup that is a proper subset of \(g\) is called a.
from www.youtube.com
Let (g, ∘) (g, ∘) be a group. the subgroup \(h = \{ e \}\) of a group \(g\) is called the trivial subgroup. First, nz is in fact a subgroup. for example, (z=2z) (z=2z) is a group with 4 elements: Let h h be a subset of g g. properties of subgroups | emathzone. Let g be a group and let g ∈ g be an element of g. The additive identity is in nz. Then (h, ∘) (h, ∘) is a subgroup of (g, ∘) (g, ∘). A subgroup that is a proper subset of \(g\) is called a.
Group Theory Proof of the Formula for the Inverse of a Product YouTube
Subgroup Proof Examples For na, nb ∈ nz, na + nb = n(a + b). First, nz is in fact a subgroup. A subgroup that is a proper subset of \(g\) is called a. The additive identity is in nz. Let g be a group and let g ∈ g be an element of g. properties of subgroups | emathzone. Let h h be a subset of g g. the subgroup \(h = \{ e \}\) of a group \(g\) is called the trivial subgroup. For na, nb ∈ nz, na + nb = n(a + b). Then (h, ∘) (h, ∘) is a subgroup of (g, ∘) (g, ∘). for example, (z=2z) (z=2z) is a group with 4 elements: The intersection of two subgroups of a group g g is a subgroup of. Let (g, ∘) (g, ∘) be a group.
From www.youtube.com
Direct Image of a Subgroup is a Subgroup Proof YouTube Subgroup Proof Examples properties of subgroups | emathzone. For na, nb ∈ nz, na + nb = n(a + b). A subgroup that is a proper subset of \(g\) is called a. The intersection of two subgroups of a group g g is a subgroup of. The additive identity is in nz. Let (g, ∘) (g, ∘) be a group. Then (h,. Subgroup Proof Examples.
From www.youtube.com
22. Subgroup in Group Theory Examples YouTube Subgroup Proof Examples First, nz is in fact a subgroup. Then (h, ∘) (h, ∘) is a subgroup of (g, ∘) (g, ∘). properties of subgroups | emathzone. The intersection of two subgroups of a group g g is a subgroup of. A subgroup that is a proper subset of \(g\) is called a. Let (g, ∘) (g, ∘) be a group.. Subgroup Proof Examples.
From printablefullcarr.z13.web.core.windows.net
Two Column Proofs Congruent Triangles Worksheet With Answers Subgroup Proof Examples Then (h, ∘) (h, ∘) is a subgroup of (g, ∘) (g, ∘). the subgroup \(h = \{ e \}\) of a group \(g\) is called the trivial subgroup. Let h h be a subset of g g. A subgroup that is a proper subset of \(g\) is called a. Let g be a group and let g ∈. Subgroup Proof Examples.
From www.youtube.com
Epimorphic Image of a Normal Subgroup Proof YouTube Subgroup Proof Examples Let g be a group and let g ∈ g be an element of g. The intersection of two subgroups of a group g g is a subgroup of. properties of subgroups | emathzone. Then (h, ∘) (h, ∘) is a subgroup of (g, ∘) (g, ∘). First, nz is in fact a subgroup. The additive identity is in. Subgroup Proof Examples.
From www.youtube.com
Group Theory Subgroup Theorem On Subgroup and Its proof One Step Subgroup Proof Examples properties of subgroups | emathzone. Let (g, ∘) (g, ∘) be a group. for example, (z=2z) (z=2z) is a group with 4 elements: For na, nb ∈ nz, na + nb = n(a + b). The intersection of two subgroups of a group g g is a subgroup of. A subgroup that is a proper subset of \(g\). Subgroup Proof Examples.
From www.youtube.com
Group Theory Two Step Subgroup Test Theorem on Subgroup and its proof Subgroup Proof Examples properties of subgroups | emathzone. A subgroup that is a proper subset of \(g\) is called a. Then (h, ∘) (h, ∘) is a subgroup of (g, ∘) (g, ∘). First, nz is in fact a subgroup. Let g be a group and let g ∈ g be an element of g. The intersection of two subgroups of a. Subgroup Proof Examples.
From www.pinterest.ph
A Group G that is Isomorphic to a Proper Subgroup Proof Maths exam Subgroup Proof Examples for example, (z=2z) (z=2z) is a group with 4 elements: Let h h be a subset of g g. Then (h, ∘) (h, ∘) is a subgroup of (g, ∘) (g, ∘). The additive identity is in nz. Let (g, ∘) (g, ∘) be a group. A subgroup that is a proper subset of \(g\) is called a. Let. Subgroup Proof Examples.
From www.youtube.com
7. Subgroup of a group Examples of subgroup Necessary and Subgroup Proof Examples The intersection of two subgroups of a group g g is a subgroup of. properties of subgroups | emathzone. Let h h be a subset of g g. A subgroup that is a proper subset of \(g\) is called a. Let (g, ∘) (g, ∘) be a group. First, nz is in fact a subgroup. the subgroup \(h. Subgroup Proof Examples.
From www.youtube.com
Proof of subgroup of cyclic group is cyclic YouTube Subgroup Proof Examples The intersection of two subgroups of a group g g is a subgroup of. properties of subgroups | emathzone. For na, nb ∈ nz, na + nb = n(a + b). Let g be a group and let g ∈ g be an element of g. First, nz is in fact a subgroup. Let (g, ∘) (g, ∘) be. Subgroup Proof Examples.
From www.youtube.com
Group Theory Subgroup Subgroup Examples Discrete Mathematics Subgroup Proof Examples for example, (z=2z) (z=2z) is a group with 4 elements: The intersection of two subgroups of a group g g is a subgroup of. Let h h be a subset of g g. properties of subgroups | emathzone. For na, nb ∈ nz, na + nb = n(a + b). Let (g, ∘) (g, ∘) be a group.. Subgroup Proof Examples.
From www.youtube.com
Definition of a Subgroup and Proof that the Kernel is a Subgroup YouTube Subgroup Proof Examples A subgroup that is a proper subset of \(g\) is called a. The intersection of two subgroups of a group g g is a subgroup of. the subgroup \(h = \{ e \}\) of a group \(g\) is called the trivial subgroup. First, nz is in fact a subgroup. For na, nb ∈ nz, na + nb = n(a. Subgroup Proof Examples.
From www.youtube.com
Centre of a group is a Subgroup of G (Theorem proof and explanation Subgroup Proof Examples A subgroup that is a proper subset of \(g\) is called a. for example, (z=2z) (z=2z) is a group with 4 elements: The additive identity is in nz. the subgroup \(h = \{ e \}\) of a group \(g\) is called the trivial subgroup. Let g be a group and let g ∈ g be an element of. Subgroup Proof Examples.
From www.youtube.com
proof special linear is a subgroup of general linear group. YouTube Subgroup Proof Examples The additive identity is in nz. For na, nb ∈ nz, na + nb = n(a + b). Let (g, ∘) (g, ∘) be a group. the subgroup \(h = \{ e \}\) of a group \(g\) is called the trivial subgroup. Let h h be a subset of g g. The intersection of two subgroups of a group. Subgroup Proof Examples.
From www.youtube.com
Group Theory The Center of a Group G is a Subgroup of G Proof YouTube Subgroup Proof Examples Then (h, ∘) (h, ∘) is a subgroup of (g, ∘) (g, ∘). the subgroup \(h = \{ e \}\) of a group \(g\) is called the trivial subgroup. properties of subgroups | emathzone. A subgroup that is a proper subset of \(g\) is called a. Let h h be a subset of g g. Let (g, ∘). Subgroup Proof Examples.
From www.slideserve.com
PPT Subgroups PowerPoint Presentation, free download ID2512510 Subgroup Proof Examples for example, (z=2z) (z=2z) is a group with 4 elements: Let h h be a subset of g g. The additive identity is in nz. properties of subgroups | emathzone. the subgroup \(h = \{ e \}\) of a group \(g\) is called the trivial subgroup. Let (g, ∘) (g, ∘) be a group. The intersection of. Subgroup Proof Examples.
From math.stackexchange.com
abstract algebra Simple Cyclic Group Proof Mathematics Stack Exchange Subgroup Proof Examples Let g be a group and let g ∈ g be an element of g. For na, nb ∈ nz, na + nb = n(a + b). Then (h, ∘) (h, ∘) is a subgroup of (g, ∘) (g, ∘). properties of subgroups | emathzone. the subgroup \(h = \{ e \}\) of a group \(g\) is called. Subgroup Proof Examples.
From www.youtube.com
Subgroup theorem proof subgroup theorem in hindi modern algebra Subgroup Proof Examples The intersection of two subgroups of a group g g is a subgroup of. A subgroup that is a proper subset of \(g\) is called a. Let (g, ∘) (g, ∘) be a group. for example, (z=2z) (z=2z) is a group with 4 elements: For na, nb ∈ nz, na + nb = n(a + b). the subgroup. Subgroup Proof Examples.
From www.youtube.com
Inverse Image of a Normal Subgroup Proof YouTube Subgroup Proof Examples Then (h, ∘) (h, ∘) is a subgroup of (g, ∘) (g, ∘). properties of subgroups | emathzone. Let (g, ∘) (g, ∘) be a group. the subgroup \(h = \{ e \}\) of a group \(g\) is called the trivial subgroup. The additive identity is in nz. for example, (z=2z) (z=2z) is a group with 4. Subgroup Proof Examples.